У цій роботі ми досліджували руйнівний вплив від вибухів на стіни з автоклавного газобетону з блоків АНБ. Спочатку були створені повнорозмірні моделі елементів газобетонної кладки, точність моделей була перевірена шляхом порівняння з результатами випробувань. Було вивчено руйнівну картину і характеристики пошкодження газобетонної стіни, а також проаналізовано вплив розміру блоків, товщини стіни, міцності на стиск розчину та відстані вибуху на ступінь руйнування газобетонних стін. Результати показали, що руйнівна картина газобетонної кладки, підданої близькому вибуху, характерна пробиванням у середині стіни. Коли масштабована відстань залишалася незмінною, площа пробивання газобетонної кладки позитивно корелювала з розміром блоків і негативно — з товщиною стіни та міцністю на стиск розчину. Коли еквівалент вибуху залишався незмінним і відстань вибуху збільшувалася, площа пробивання спочатку збільшувалася, а потім зменшувалася. Відповідно до механізму пошкодження газобетонної кладки було розроблено метод розрахунку для прогнозування площі пробивання газобетонної кладки, і точність цього методу була перевірена шляхом порівняння з числовими результатами. Крім того, було розроблено критерій пошкодження на основі площі пробивання для визначення рівнів руйнування газобетонних кладок.
З огляду на зростання частоти терористичних атак та випадкових вибухів у будівлях за останні роки, стійкість до вибухів важливих економічних об'єктів та звичайних цивільних будівель стала потенційною вимогою та викликом для інженерних та академічних спільнот. Кладка стін, яка є значущим компонентом будівлі, виконує функції огородження та розділення простору. Кладка стін, яка складається з анізотропної шаруватої структури, утвореної блоками з низькою міцністю та розчином, зазнає серйозних пошкоджень через її крихку природу та низьку цілісність під дією вибухового навантаження, а утворені уламки та витік тиску неминуче спричиняють жертви та травми серед мешканців і серйозні пошкодження обладнання всередині будівлі. Тому існує нагальна потреба вивчати динамічну відповідь та вплив пошкоджень кладок стін під дією вибухового навантаження, щоб забезпечити захист від вибухів.
Дослідники по всьому світу вивчали аналіз впливу пошкоджень кладок стін під дією вибухового навантаження. Ахмад та ін. провели шість випробувань на великих відстанях, щоб вивчити динамічну відповідь кладок стін з керамічної цегли під дією вибухового навантаження, тоді як Нок та ін. виконали випробування вибуху на близькій відстані, щоб дослідити закон розподілу уламків стін під дією вибухового навантаження та отримали емпіричну формулу для прогнозування швидкості уламків на основі експериментальних даних. Ши та ін. провели два випробування на близькій відстані стінами з керамічної цегли, щоб проаналізувати механізм пошкодження та характеристики дроблення, і результати показали, що розподіл розмірів дрібних фрагментів підпорядковувався розподілу Вейбулла. Лі та ін. провели експерименти для оцінки ступеня пошкодження стін з керамічної цегли під дією вибуху природного газу, і результати показали, що зі збільшенням товщини стіни або зменшенням висоти стіни максимальне зміщення та рівень пошкодження кладок стін значно зменшувалися.
Зі значними поліпшеннями обчислювальної потужності в останні роки, технологія числового моделювання широко використовується для дослідження вибухової відповіді кладок стін. Шамім та ін. провели серію досліджень динамічної відповіді різних типів кладок стін під дією вибухового навантаження з використанням числових методів. Результати показали, що еквівалент вибуху, відстань до вибуху, висота детонації та кут детонації суттєво впливали на рівень пошкодження кладок стін. Крім того, було розроблено числові алгоритми для опису характеристик пошкоджень кладок стін та масштабовані методи числового моделювання для покращення точності числового моделювання та обчислювальної ефективності незалізобетонних кладок стін під дією вибухового навантаження.
Як новий штучний стіновий матеріал (ред. - для Китаю), автоклавний газобетон (АНБ) широко використовується в кладках стін різних будівель завдяки відмінним будівельним характеристикам, низькому співвідношенню маси до міцності, хорошій теплоізоляції та властивостям поглинання енергії. З огляду на відмінності в сировинних матеріалах та виробничих процесах, механічні властивості блоків АНБ суттєво відрізняються від традиційної керамічної цегли, що привертає широку увагу дослідників у всьому світі. Го та ін. провели серію випробувань на зменшення ваги для оцінки динамічної міцності та характеристик поглинання АНБ. Дослідження показало, що крива напруження-деформації АНБ складалася з трьох стадій під дією низькошвидкісного удару, з незначним впливом швидкості навантаження на динамічну міцність. Фенг та ін. провели випробування на динамічну міцність на стиск АНБ з різними густинами в діапазоні швидкості деформації 60–250 с⁻¹, використовуючи систему розділеного стрижня Гопкінсона. Результати показали очевидне підвищення динамічної міцності на стиск АНБ зі збільшенням густини. Нян та ін. оцінили динамічну відповідь AНБ під дією вибухової ударної хвилі, створеної ударною трубою, і результати показали суттєвий вплив порової структури та подальшого збільшення густини AНБ у нелінійній залежності напруження-деформація.
Через потенційну загрозу звичайних видів зброї та випадкових вибухів стійкість до вибухів та динамічна відповідь кладок стін під дією вибухового навантаження отримали значну увагу. Янкелевський та Авнон провели серію експериментів на локальну відповідь AНБ під контактним вибухом, зосереджуючись на ефекті армуванням тканиною з полівініл ацетат (PVA). Результати показали, що міцність на розтяг та пластичність AНБ були ефективно покращені за рахунок тканини, що підвищило стійкість до розтріскування на розтяг AНБ. Лі та ін. провели випробування та числові моделювання для оцінки впливу міцності блоків, граничних умов та товщини на стійкість до вибухів кладок стін AНБ під дією вибухів природного газу. За результатами дослідження, вплив товщини та габаритів на динамічну відповідь стін AНБ був значним, тоді як вплив міцності AНБ на стійкість до вибухів був мінімальним. Ю та ін. провели випробування для дослідження режиму руйнування кладок стін AНБ віддаленими вибухами, та були встановлені критерії оцінки пошкоджень стін AНБ на основі режимів руйнування зразків. Сомаєх та ін. проаналізували стійкість до вибухів кладок стін AНБ під дією віддалених вибухів за допомогою числових методів, і були визначені впливи товщини стін та масштабованої відстані на динамічну відповідь стін.
Дослідження стійкості до вибухів кладок стін здебільшого зосереджені на віддалених вибухах з відстанню більше двох метрів від епіцентру вибуху. Через різні розподіли вибухового навантаження на поверхнях кладок стін, ці результати досліджень не можуть точно вказувати на динамічну відповідь та пошкодження кладок стін під близькими вибухами з відстанню менше двох метрів. Крім того, дослідження факторів впливу стійкості до вибухів кладок стін AНБ, особливо ступеня ефективності розміру блоків та механічних властивостей матеріалів кладки, не було комплексним. Нарешті, існуючі методи оцінки пошкоджень та критерії руйнування кладок стін здебільшого застосовувалися до кладок стін з керамічної цегли. Через відмінності в механічних властивостях блокових матеріалів та різні механізми руйнування стін під дією вибухового навантаження ці критерії оцінки не можуть точно оцінити стійкість до вибухів кладок стін AНБ.
Перевірка числової моделі
Через високу швидкість розповсюдження, високий піковий тиск та коротку тривалість, динамічна відповідь та режими руйнування блоків з газобетону (АНБ) суттєво відрізняються від таких під статичним навантаженням. Ю та ін. провели тести на динамічну відповідь і пошкодження кладки стін з газобетону під дією вибухового навантаження, де під час випробування заряд масою 3000 кг тротилового еквівалента був розташований на відстані 70 м перед стіною з газобетону. Зразки стін з газобетону розмірами 3,6 × 3,6 × 0,2 м і експериментальна установка показані на рис. 1. Основні механічні параметри газобетону були такими: одноосьова міцність на стиск становила 3,5 × 10⁶ Па, модуль Юнга – 5,3 × 10⁸ Па, коефіцієнт Пуассона – 0,2, середня густина – 500 кг/м³, а розміри блоку – 0,6 × 0,6 × 0,2 м. Розчин мав міцність на стиск 7,6 × 10⁶ Па. Після цього динамічна відповідь і пошкодження стіни з газобетону під дією вибухового навантаження були змодельовані для перевірки надійності та точності числової моделі.
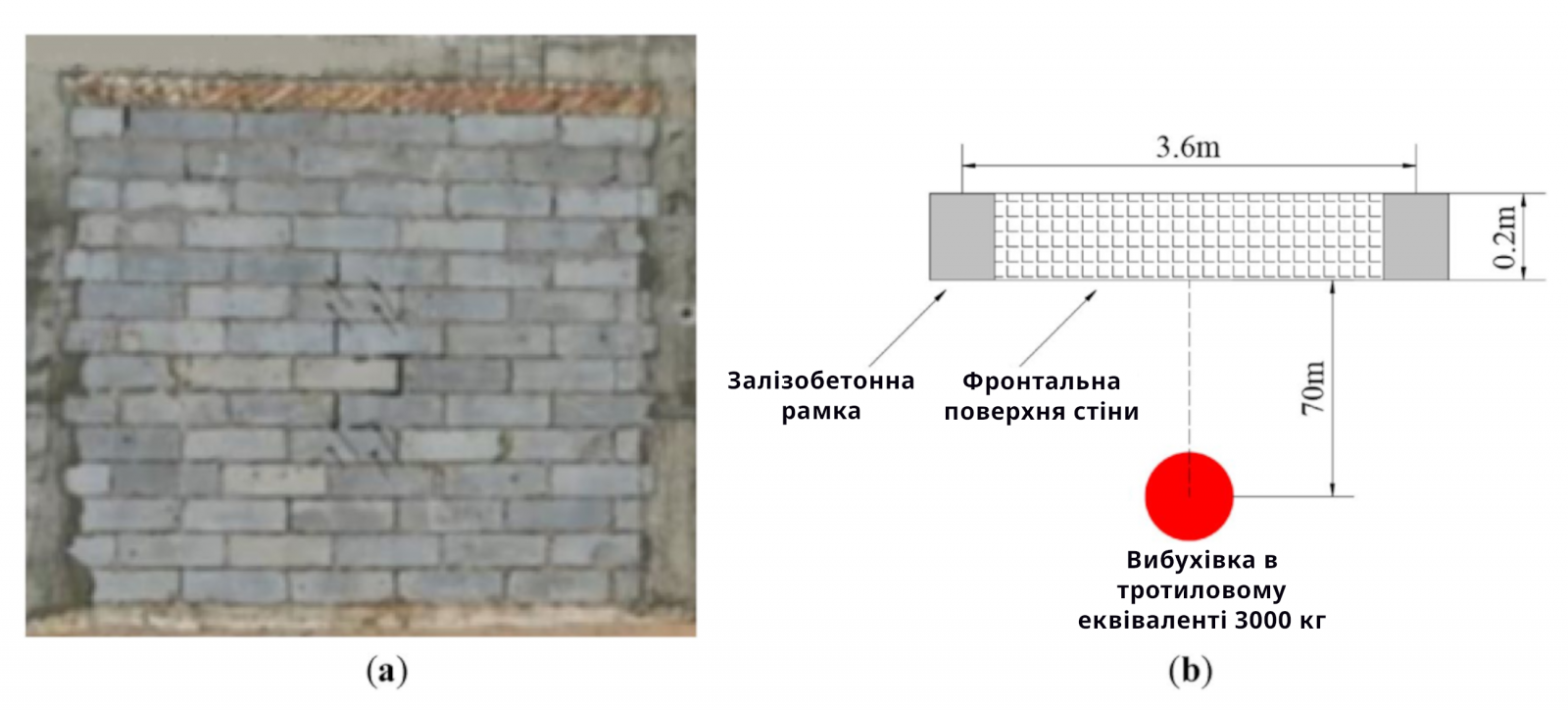
Рисунок 1. (a) Зразок стіни з газобетону (АНБ); (b) налаштування тесту.
Модель скінченних елементів
Числова модель кладки стіни з газобетону (АНБ) була розділена на модель розділення та модель гомогенізації. Модель розділення була створена шляхом окремого розгляду блоків та розчину, щоб точно моделювати процеси зсуву та руйнування між блоками та розчином. Через незначну різницю в механічних властивостях між газобетоном і розчином контактну поверхню нульової товщини можна застосувати для заміни розчину. У цьому розділі була розроблена модель розділення кладки стіни з газобетону, використовуючи комерційне програмне забезпечення для моделювання скінченних елементів LS-DYNA, як показано на рис. 2. Для блоків з газобетону та зовнішньої рами використовували метод Лагранжа, де координати переміщувалися разом з матеріалом, і всі зміщення вузлів та обертання бетонної рами були зафіксовані.
Модель матеріалу
Для моделювання блоків з газобетону (АНБ) використали модель матеріалу *Mat_96 (MAT_BRITITLE_DAMAGE). Ця модель складалася з анізотропної моделі крихкого руйнування, яка могла застосовуватися до різноманітних крихких матеріалів. Відповідно до стандарту випробувань GB/T11971-1997, Лі та інші вилили зразки кубів з газобетону розміром 0,1 м і використали сервогідравлічну випробувальну машину MTS для оцінки механічних властивостей зразків з газобетону та визначення параметрів моделі матеріалу для блоків з газобетону. Міцність на розтяг, міцність на зсув, енергія руйнування та коефіцієнт утримання зсуву були отримані з джерела 30, тоді як густина, межа текучості на стиск, модуль пружності та коефіцієнт Пуассона були отримані з джерела 32. Детальні значення параметрів моделі наведено в таблиці 1. Для точного моделювання руйнування стіни з газобетону під дією вибухового навантаження та запобігання надмірної деформації елементів використовувалися критерії ерозії для моделювання руйнування матеріалів. Максимальна головна деформація використовувалася як критерій руйнування, і значення було визначено як 0,01. Варто зазначити, що значення деформації руйнування не мало відповідної теоретичної основи і було визначено головним чином шляхом пробних розрахунків у цьому дослідженні.
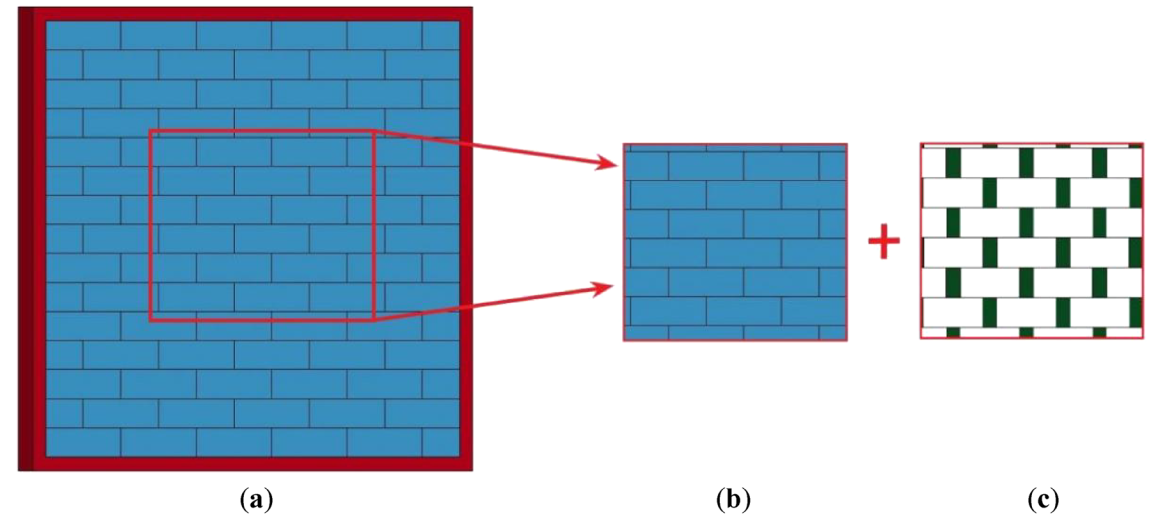
Рисунок 2. (a) Цілісна модель; (b) модель блоку; (c) модель розчину.
| Густина (кг/м3) |
Модуль Юнга (Па) | Коефіцієнт Пуассона | Міцність на розрив (Па) | Міцність на зсув (Па) | Текучість при стисненні (Па) | Енергія руйнування (Н/м) |
Фактор утримання зсуву |
| 500 | 6.3 × 108 | 0,2 | 7 × 105 | 1 × 106 | 3 × 106 | 80 | 0,03 |
Таблиця 1. Параметри матеріалів для блоків АНБ.
Через високу міцність і жорсткість зовнішньої рами, у попередніх тестах мінімальні пошкодження виникали на зовнішній рамі. Крім того, дослідницьким об'єктом цієї числової моделі були поведінка пошкоджень та динамічна відповідь. Тому для моделювання зовнішньої рами була застосована модель Rigid.
Метод застосування навантаження
Метод зв'язування рідина–тверде тіло та метод CONWEP зазвичай використовуються для застосування вибухового навантаження. Метод зв'язування рідина–тверде тіло міг встановлювати повітряний домен і розраховувати процес поширення вибухової ударної хвилі в повітрі. Метод CONWEP спрощував ці процеси, що ефективно знижувало складність моделі скінченних елементів і підвищувало ефективність розрахунків. Тому метод CONWEP був використаний для застосування вибухових навантажень з різними значеннями маси тротилу та різними відстанями вибуху до кладки стіни з газобетону.
CONWEP, метод розрахунку вибухового навантаження, розроблений на основі апроксимації великої кількості експериментальних даних, був побудований за допомогою програми LS-DYNA, і вибухове навантаження було застосоване до вибраної поверхні за допомогою ключових слів *LOAD_BLAST_ENHANCED та *LOAD_BLAST_SEGMENT. Криву часу надлишкового тиску можна було представити за допомогою модифікованого рівняння Фрідлендера, відповідно до
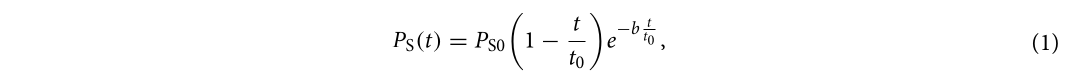
де PS0 - це піковий інцидентний надлишковий тиск, t0 - це тривалість позитивної фази, а b - коефіцієнт затухання хвилі. Піковий надлишковий тиск на конструкцію також залежав від кута падіння θ. Метод CONWEP міг генерувати еквівалентне значення надлишкового тиску, як це виражено
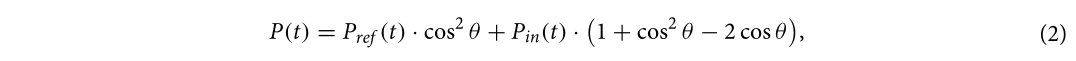
де Pref - це відбивний тиск, а Pin - інцидентний тиск, який можна розрахувати за рівнянням (1).
Контактна поверхня
Зв'язок між блоками AНБ, а також між стіною АНБ і зовнішньою рамою був змодельований як контакти з розривом у числовій моделі, щоб точно описати розділення і ковзання між контактними поверхнями. Контакт був досягнутий за допомогою команди *TIEBREAK_SURFACE_TO_SURFACE в LS-DYNA. Цей контакт керувався критерієм руйнування на основі напруги, відповідно до
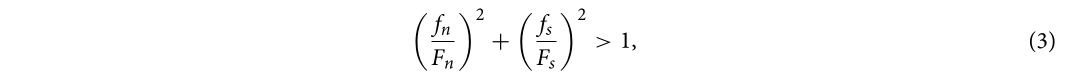
де fn і fs позначають нормальну напругу і зсувну напругу на контактній поверхні відповідно, а Fn і Fs - це нормальна гранична напруга і зсувна гранична напруга відповідно, які можна охарактеризувати міцністю розчину на розтяг і зсув. Коли стан напруги на контактній поверхні задовольняв рівнянню (3), взаємний контактний рух між блоками обмежувався б тертям. У цьому дослідженні статичні і динамічні коефіцієнти тертя становили 0.4 і 0.3 відповідно, тоді як нормальна гранична напруга Fn і зсувна гранична напруга Fs були 3 × 105 Па. Вищезазначені параметри були отримані шляхом пробних розрахунків і підтверджені експериментальними даними.
Розмір сітки
У числових симуляціях, які моделювали взаємодії між вибуховим навантаженням і кладкою стіни, точність числових результатів значною мірою залежала від розміру сітки моделі скінченних елементів. Щоб забезпечити точність числових результатів, був проведений аналіз збіжності розміру сітки моделі скінченних елементів, щоб визначити відповідні параметри в цьому розділі.
Було побудовано три моделі скінченних елементів стіни з газобетону з розмірами сітки 0,01, 0,02 і 0,05 м для моделювання взаємодій між вибуховим навантаженням і стіною з газобетону. На рисунку 3 показано кінцеве руйнування моделей скінченних елементів з різними розмірами сітки, коли еквівалент вибуху становив 1 кг, а відстань вибуху - 0,5 м. Із зменшенням розміру сітки кінцеве руйнування стіни з газобетону схильне до збіжності. Однак було виявлено, що чим дрібніша сітка, тим точніше розраховується кінцеве руйнування стіни з газобетону. Враховуючи точність розрахунків і обчислювальну ефективність, був обраний розмір сітки 20 мм, а модель скінченних елементів мала загалом 280 000 твердих елементів, 353 265 вузлів і 1 485 000 ступенів свободи.
Порівняння експериментальних і числових результатів
Кінцеве руйнування стіни з газобетону в тесті показано на рисунку 3. На поверхнях деяких блоків на краю стіни з газобетону спостерігалося фрагментація і відшаровування, а в центральній частині стіни з газобетону утворився квадратний отвір розміром 1,2 × 1,2 м. Відносно цілі блоки газобетону відпали спереду і ззаду стіни, що було зумовлено головним чином руйнуванням клейового розчину. На рисунку 4 показано кінцеве руйнування стіни з газобетону в числовому розрахунку. Через руйнування елементів і переміщення блоків після руйнування контактної поверхні в центральній частині стіни утворився прямокутний отвір розміром 1,3 × 1,2 м. Режим руйнування і площа пошкодження стіни з газобетону в числовому розрахунку в основному збігалися з експериментальними результатами, що підтвердило точність числової моделі і параметрів матеріалу.
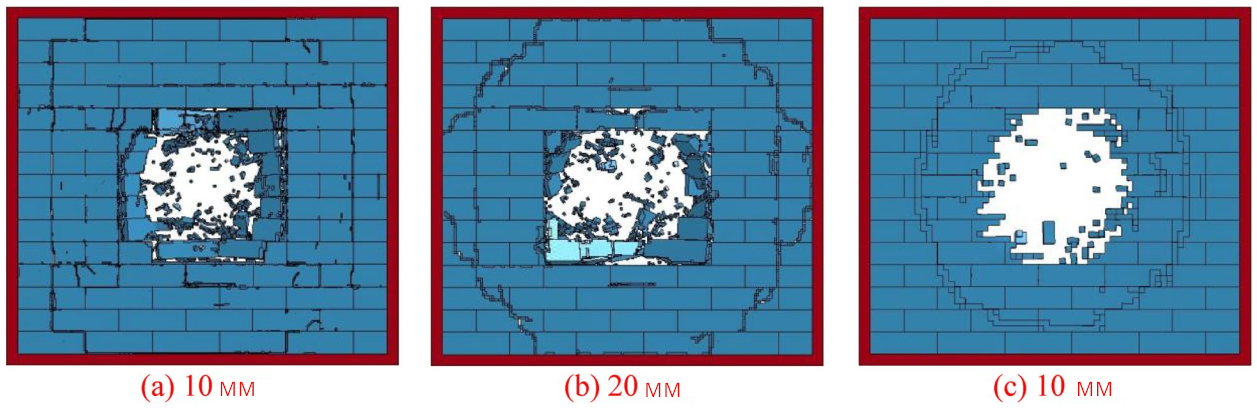
Рисунок 3. Кінцеве руйнування, визначене за допомогою моделей скінченних елементів з різними розмірами сітки.
Динамічна відповідь стіни з газобетону (АНБ) при вибуху в безпосередній близькості
У цьому розділі було проведено чисельне моделювання динамічної відповіді та руйнування стіни з газобетону (АНБ) при вибуховому навантаженні в безпосередній близькості. На основі результатів моделювання було проаналізовано характеристики динамічної відповіді та режими руйнування стіни з газобетону при вибуховому навантаженні в безпосередній близькості. Крім того, було оцінено вплив таких параметрів, як розмір блоків, товщина стіни, міцність на стиск розчину та відстань від місця вибуху до стіни на динамічну відповідь та руйнування стіни з газобетону при вибуху в безпосередній близькості.
Типові результати моделювання
Як типовий зразок було обрано стіну з газобетону шириною 3,3 м, висотою 3,0 м і товщиною 0,2 м. Розміри блоків з газобетону становили 600 × 200 × 200 мм, а міцність на стиск — 3,5 × 106 Па. На рисунку 5 показано серію ізоповерхонь переміщення в різні моменти часу, включаючи переміщення блоків у три моменти часу, що чітко показує руйнування та переміщення блоків. У момент t = 0,01 с енергія, що утворилася внаслідок вибуху, була поглинута стіною і поширювалася у вигляді хвиль напруження в стіні. У середній частині стіни спостерігалося серйозне пробивне руйнування. У крайній частині передньої поверхні вибуху спостерігалося незначне руйнування через стискання, а на задній поверхні вибуху відбувалося відшарування під дією хвилі розтягувального напруження. У момент t = 0,05 мс пошкодження стіни з газобетону ще більше посилилося, і напруження на контактній поверхні між деякими блоками в крайній частині перевищило межу зсуву, що призвело до переміщення блоків від стіни. У момент t = 0,2 с пробивне руйнування частини стіни з газобетону ще більше розширилося, і в середній частині стіни утворився прямокутний отвір через пошкодження та зсув блоків. Згідно з чисельними результатами, контактна поверхня між блоками була вразливою частиною при вибуховому навантаженні в безпосередній близькості, яка була схильна до пошкоджень, а пошкодження стіни відбувалося у формі пробивного руйнування.

Рисунок 4. (a) Експериментальні результати 32; (b) чисельні результати.
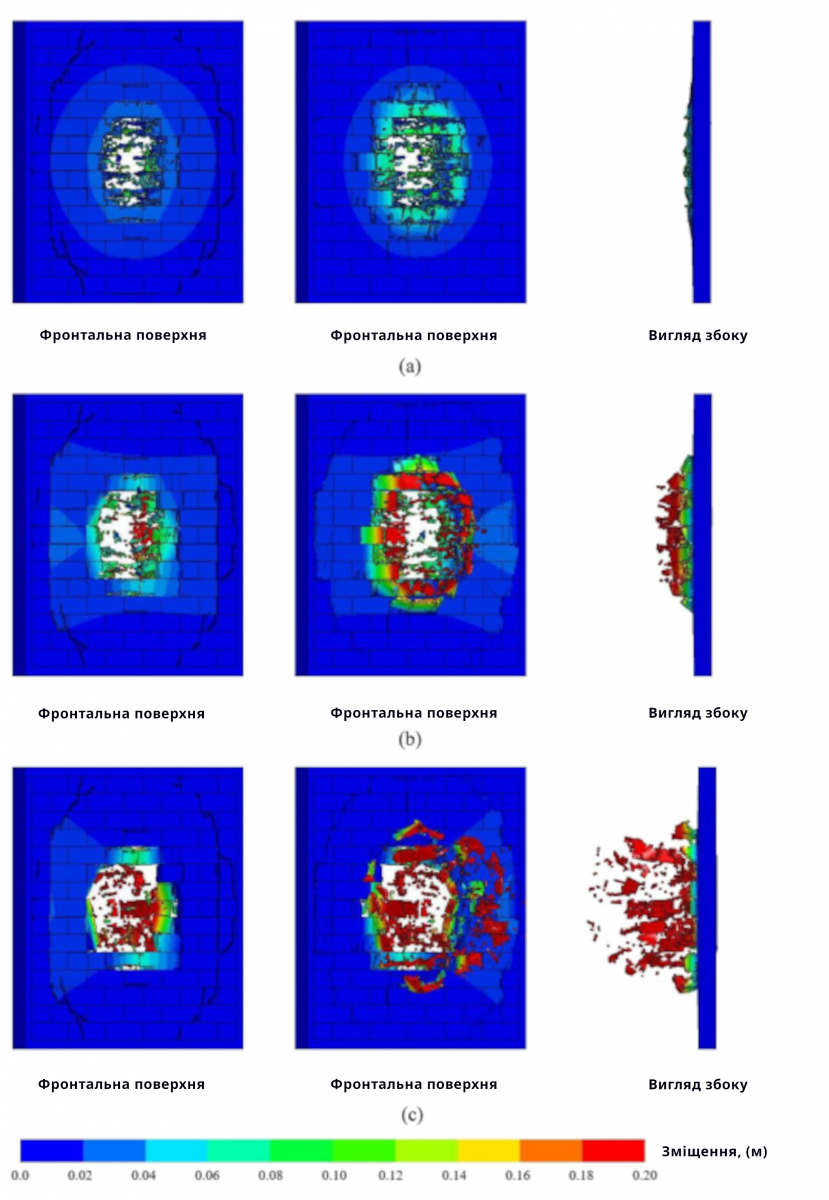
Рисунок 5. (a) Зміщена хмара кладки стіни AНБ при t = 0,01 с;
(b) Зміщена хмара кладки стіни AНБ при t = 0,05 с; (c) Зміщена хмара кладки стіни AНБ при t = 0,2 с.
Дослідження параметрів
Стіна з газобетону (АНБ) складалася з блоків і розчину, а вибухостійкість стіни залежала від розмірів блоків і механічних властивостей розчину. Крім того, для однієї і тієї ж маси заряду ТНТ розподіл тиску на поверхні стіни змінювався залежно від відстані вибуху. У цьому розділі обговорювалися впливи розмірів блоків, товщини стіни, міцності на стиск розчину та відстані вибуху на динамічну реакцію та ступінь пошкодження стіни з газобетону під дією близького вибуху.
Вплив розміру блоків
Щоб дослідити відмінності у вибухостійкості стіни з газобетону при різних розмірах блоків, були створені шість моделей з різними розмірами блоків. Розмір сітки та параметри матеріалу відповідали розділу "Динамічна реакція стіни з газобетону під дією близького вибуху". У прикладах розрахунків відстань від заряду ТНТ до центру стіни становила 0,5 м, а еквівалент вибуху - 1 кг.
Таблиця 2 показує площу відшарування та площу пробивного отвору стіни з газобетону. Коли кількість блоків збільшилася з 60 до 255, площа відшарування передньої поверхні вибухової стіни зменшилася на 20,7%, а площа пробивного отвору - на 8,8%. Причина цього полягає в тому, що коли розміри стіни були однакові, а розмір блоків зменшувався, кількість розчину для зв'язування кладки збільшувалася, і вибухова енергія, поглинена розчином, також збільшувалася. Завдяки більшій міцності розчину порівняно з блоками, ступінь пошкодження стіни з газобетону зменшувався.
На малюнку 6 показано остаточні пошкодження стін з газобетону при різних розмірах блоків під час близького вибуху, що показує, що площа відшарування та пробивного отвору стіни з газобетону були майже симетрично розподілені навколо центру стіни. Коли довжина блоку була постійною, поперечний розмір пробивного отвору був однаковий, а бічний розмір був цілим кратним висоти блоку. Коли висота блоку була постійною, бічний розмір пробивного отвору був однаковий, а поперечний розмір пробивного отвору в кладці зі стіною з невеликим розміром блоків та однаковою довжиною та висотою був цілим кратним довжини блоку. Крім того, поперечний розмір пробивного отвору для кладки з великим розміром блоків і співвідношенням сторін більше одного був напівцілим кратним довжини блоку. Причина цього явища полягає в тому, що при малому розмірі блоку з більшою бічною жорсткістю та поздовжньою жорсткістю блоки не схильні до пробивного руйнування. Коли висота блоків була невеликою, а довжина великою, бічна жорсткість була нижчою за поздовжню жорсткість, і в середині блоків відбувалося зсувне руйнування. Як уразлива частина стіни з газобетону, шар зв'язування між блоками пошкоджувався першим під дією близького вибухового навантаження, що спричиняло переміщення блоків. Тому бічний розмір пробивного отвору стіни з газобетону був цілим або напівцілим кратним довжини блоків, а поздовжній розмір був цілим кратним висоти блоку.
Підсумовуючи, зі зменшенням розміру блоку ефект зсувної стійкості блоку збільшувався, а площа пробивного отвору стіни з газобетону зменшувалася, тоді як форма пробивного отвору змінювалася з прямокутної на приблизно круглу. Однак чисельні результати також показали, що зменшення розміру блоку мало обмежений вплив на покращення вибухостійкості стіни з газобетону.
| Розмір блоку, м | Кількість блоків | Площа контактної поверхні між блоками та клейовим розчином, м2 | Площа відшарування, м2 | Площа пробитого отвору, м2 |
| 0.60 × 0.30 × 0.20 | 60 | 20.4 | 8.28 | 1.71 |
| 0.60 × 0.20 × 0.20 | 90 | 27.0 | 7.84 | 1.77 |
| 0.60 × 0.15 × 0.20 | 120 | 33.6 | 7.02 | 1.70 |
| 0.40 × 0.20 × 0.20 | 135 | 30.6 | 6.65 | 1.64 |
| 0.20 × 0.20 × 0.20 | 255 | 40.2 | 6.56 | 1.56 |
Таблиця 2. Пошкодження стін з газобетону з різними розмірами блоків під час вибуху впритул.
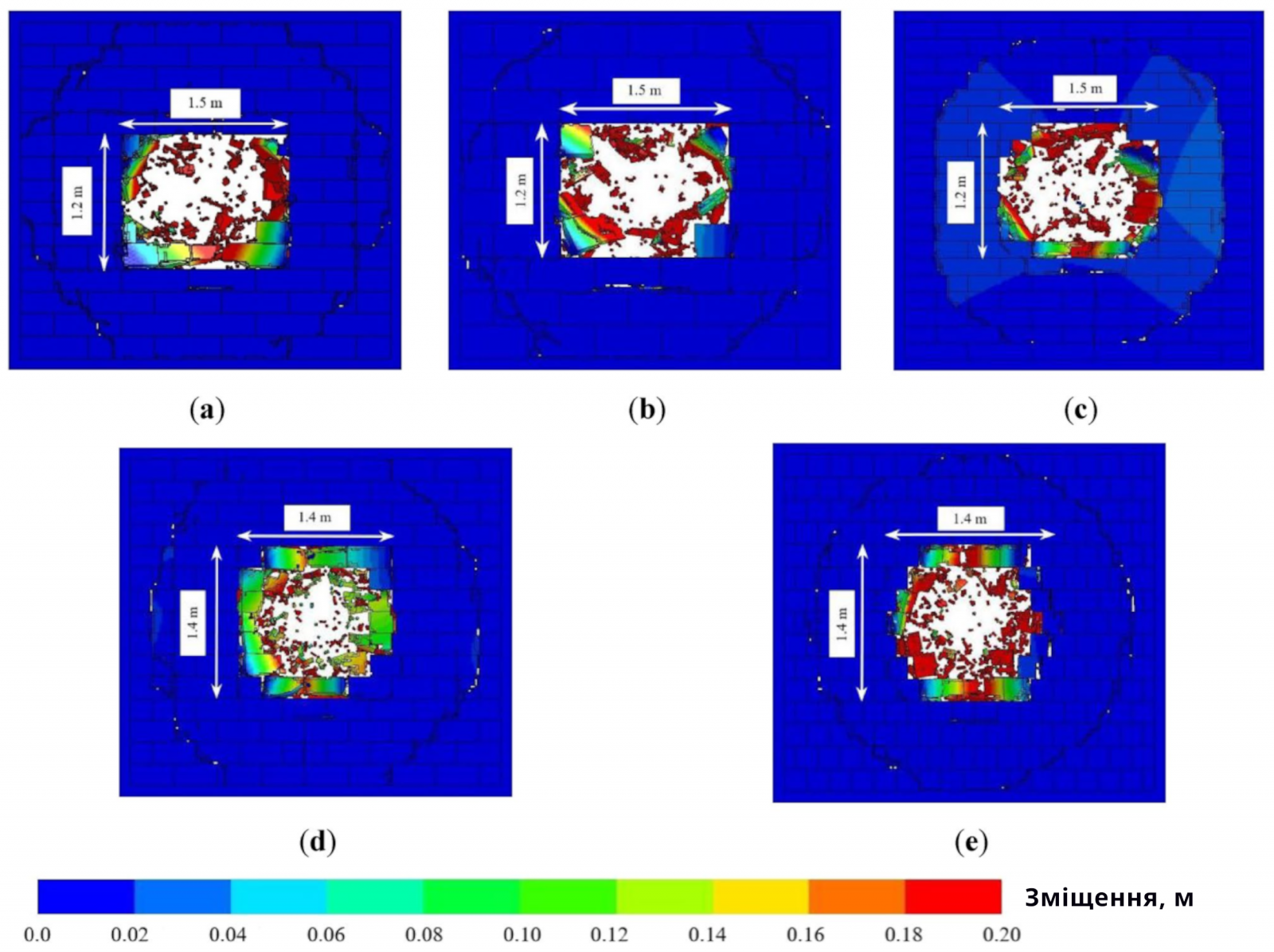
Рисунок 6. (а) Остаточне пошкодження стіни АНБ розміром блоку 0,60 × 0,20 × 0,20 м;
(b) остаточне пошкодження стіни АНБ розміром блоку 0,60 × 0,30 × 0,20 м;
(c) остаточне пошкодження стіни АНБ розміром блоку 0,60 × 0,15 × 0,20 м;
(d) остаточне пошкодження стіни АНБ розміром блоку 0,40 × 0,20 × 0,20 м;
(e) остаточне пошкодження стіни АНБ розміром блоку 0,20 × 0,20 × 0,20 м.
Вплив товщини стіни
Динамічні реакції та ефекти пошкодження стін з газобетону з різною товщиною під дією однакового вибуху відрізнялися. Щоб дослідити вплив товщини на динамічну реакцію та ефект пошкодження стіни з газобетону під дією вибухового навантаження, було створено п'ять чисельних моделей стіни з газобетону з товщинами 100, 150, 200, 250 та 300 мм. Розмір сітки та параметри матеріалу відповідали розділу "Верифікація чисельної моделі". Відстані від заряду ТНТ до стіни становили 0,5 і 2,0 м, відповідно, а еквівалент вибуху - 1 кг.
| Еквівалент вибухівки (кг) | Відстань заряду (м) | Товщина стіни (мм) | Остаточний стан пошкодження |
| 1 | 0.5 | 0.10 | Пробиваючі пошкодження в загальній площі, де площа отвору пробивання становила 8.31 м2 |
| 0.15 | Пробиваючі пошкодження в загальній площі, де площа отвору пробивання становила 7.82 м2 |
||
| 0.20 | Пробиваючі пошкодження в середній області, де площа отвору пробивання становила 1.96 м2 |
||
| 0.25 | Пробиваючі пошкодження в середній області, де площа отвору пробивання становила 0.94 м2 |
||
| 0.30 | Пробиваючі пошкодження в середній області, де площа отвору пробивання становила 0.78 м2 |
||
| 1 | 2.0 | 0.10 | Невеликі пошкодження, де максимальне зміщення 2.3 × 10−2 м |
| 0.15 | Пружна деформація, де максимальне зміщення 8.7 × 10−4 м |
||
| 0.20 | Пружна деформація, де максимальне зміщення 4.2 × 10−4 м |
||
| 0.25 | Пружна деформація, де максимальне зміщення 1.7 × 10−4 м |
||
| 0.30 | Пружна деформація, де максимальне зміщення 8.0 × 10−5 м |
Таблиця 3. Кінцевий стан ушкоджень стіни з кладки газобетону різної товщини.
Таблиця 3 підсумовує остаточний стан пошкодження стіни з газобетону різної товщини. Коли відстань вибуху становила 0,5 м, у стінах з газобетону з різною товщиною спостерігалося пробивне руйнування. Зі збільшенням товщини стіни з 0,1 до 0,3 м площа пробивного отвору зменшилася на 90,6%. Коли відстань вибуху становила 2,0 м, середня область стіни з товщиною 0,1 м була злегка пошкоджена, а динамічна реакція інших стін залишалася в межах пружної деформації. Зі збільшенням товщини стіни з 0,1 до 0,3 м максимальне переміщення стіни зменшилося на 99,6%. Причина цього явища полягала в тому, що зі збільшенням товщини стіни інерційний момент перерізу, паралельний до напрямку вибухового навантаження, та сила зв'язування між розчином і блоками збільшувалися. Таким чином, зсувна здатність стіни значно покращувалася, що підвищувало її вибухостійкість.
На малюнку 7 показано остаточний стан пошкодження стін з різною товщиною при відстані вибуху 0,5 м, де B позначає товщину стіни. Коли товщина стіни становила 0,10 м, блоки в середній частині стіни були розчавлені через перевищення тиску над міцністю матеріалу, а навколишня область була викинута з рами в цілісній формі, і площа пробивного отвору була приблизно круглою. Коли товщина стіни збільшувалася до 0,15 м, площа пробивного отвору відносно зменшувалася, а її форма залишалася приблизно круглою. З подальшим збільшенням товщини стіни спостерігалося лише незначне відшарування в навколишній області стіни. Діапазон розчавлених блоків у середній частині стіни поступово зменшувався, а форма пробивного отвору змінювалася з круглої на квадратну. Причина цього явища полягає в тому, що при невеликій товщині стіни зсувна стійкість стіни була низькою, і блок був схильний до пробивного руйнування з формою розподілу вибухового навантаження. Тому пробивний отвір був приблизно круглим. Зі збільшенням товщини стіни зсувна стійкість стіни покращувалася, і середина блоку та контактні поверхні між блоком і розчином були уразливими. Внаслідок цього при високому вибуховому навантаженні відбувалося зсувне руйнування. Тому пробивний отвір був приблизно квадратним.
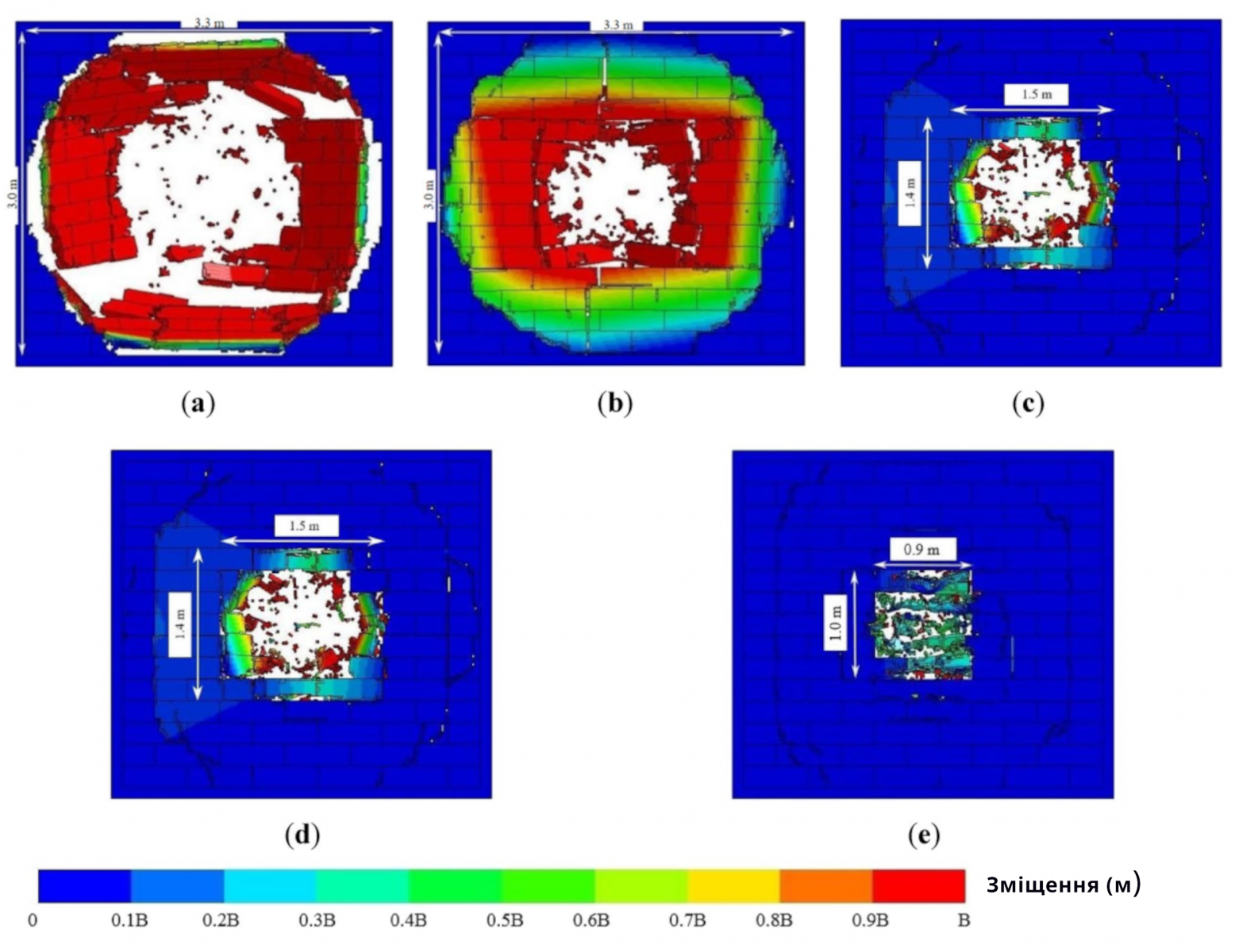
Рисунок 7. (a) Остаточне пошкодження стіни з газобетону товщиною 0,10 м;
(b) Остаточне пошкодження стіни з газобетону товщиною 0,15 м;
(c) Остаточне пошкодження стіни з газобетону товщиною 0,20 м;
(d) Остаточне пошкодження стіни з газобетону товщиною 0,25 м;
(e) Остаточне пошкодження стіни з газобетону товщиною 0,30 м.
Вплив міцності розчину на стиск
Міцність розчину на стиск є ключовим фактором, що впливає на вибухостійкість стіни з газобетону (АНБ). Для аналізу впливу міцності розчину на стиск на ступінь пошкодження стіни при близькому вибуху було створено чотири числові моделі стін з газобетону з міцністю розчину на стиск 2.5, 5, 7.5 та 10 МПа. Кількість вибухівки TNT становила 1 кг, а відстані до вибуху - 0,5 та 0,2 м, де відповідні масштабовані відстані становили 0,5 та 2 м/кг1/3. У цьому розділі розчин з різною міцністю на стиск був отриманий шляхом зміни значень нормальної напруги руйнування та напруги зсуву в контакті TIEBREAK. Рівняння (4) та (5) представляють методи розрахунку середньої міцності на розтяг σt та середньої міцності на зсув σv кладки вздовж прямого стику відповідно до китайського стандарту GB55007-2021:
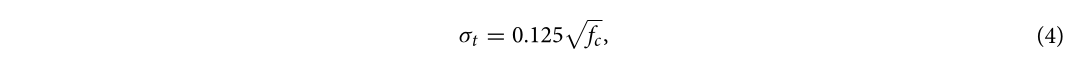
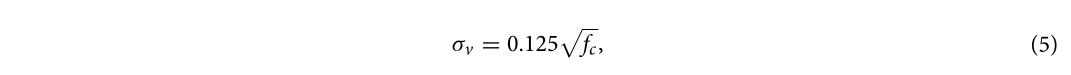
де fc - міцність розчину на стиск.
На рисунку 8 показано кінцеве пошкодження стіни з газобетону при різних міцностях розчину на стиск, коли масштабована відстань становила 0,5 м/кг1/3. Коли міцність на стиск становила 2,5 × 106 Па, часткове зв'язування між стіною та каркасом було пошкоджено, а на крайових ділянках передньої та задньої вибухових поверхонь стіни спостерігалося серйозне лущення. Крім того, в центральній частині стіни з'явилася пробивна діра. Коли міцність на стиск становила 5,0 × 106 Па, тріщини на зв'язках між стіною та каркасом не з'явилися. Площі лущення передньої та задньої вибухових поверхонь стіни зменшилися на 12,1%, а площа пробивної діри зменшилася на 23,0%. Коли міцність на стиск була збільшена до 1,0 × 107 Па, площі лущення передніх та задніх вибухових поверхонь стіни зменшилися на 46,4%, а площа пробивної діри зменшилася на 65,5%. Це свідчило про те, що ступінь пошкодження стіни з газобетону зменшувався зі збільшенням міцності розчину на стиск.

Рисунок 8. (a) Міцність розчину на стиск 2,5 × 106 Па;
(b) міцність розчину на стиск 5,0 × 106 Па;
(c) міцність розчину на стиск 7,5 × 106 Па;
(d) міцність розчину на стиск 1,0 × 107 Па.
На рисунку 9 показано порівняння різних міцностей розчину на стиск з кривими зміщення та швидкості в часі центру стіни з газобетону при масштабованій відстані 2 м/кг1/3. За цим вибуховим навантаженням, динамічна відповідь стіни з газобетону перебувала в межах еластичності. Зі збільшенням міцності розчину на стиск, піки зміщення та швидкості центру стіни поступово зменшувалися, частота вібрації поступово збільшувалася, а час повернення стіни до статичного стану поступово зменшувався.
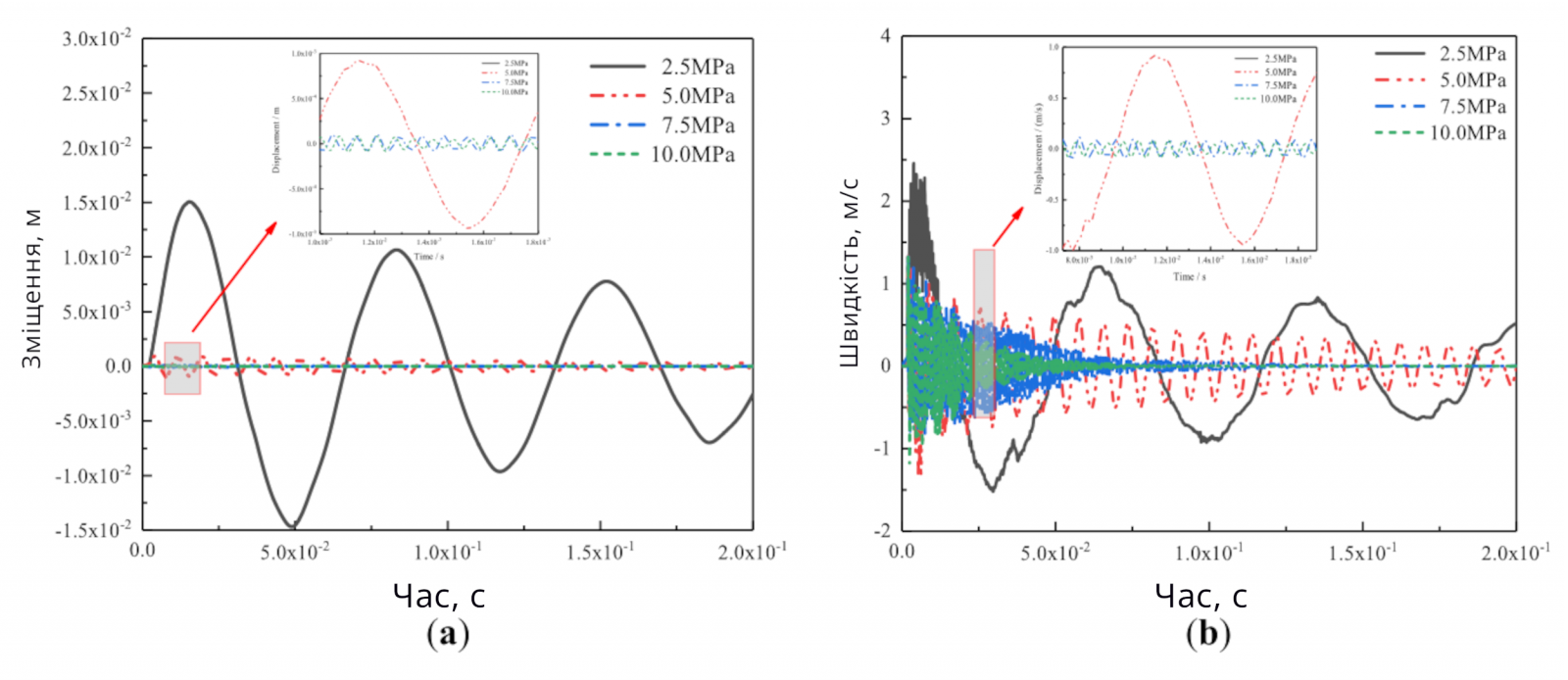
Рисунок 9. (a) Крива історії переміщення в часі; (b) крива швидкості в часі.
Вищезгаданий аналіз показав, що зі збільшенням міцності розчину на стиск, міцність поверхні зв'язування між блоком та розчином зростала, що призводило до збільшення цілісності стіни з газобетону та підвищення ефекту розсіювання енергії вибуху. Максимальне зміщення та ступінь пошкодження стіни зменшувалися. Таким чином, підвищення міцності розчину на стиск дозволяло стіні підвищити стійкість до вибухових пошкоджень.
Вплив відстані вибуху
При однаковому еквіваленті вибуху розподіл тиску та імпульсу на поверхні стіни змінювався зі зміною відстані вибуху. Щоб дослідити вплив відстані вибуху на ступінь пошкодження стіни з газобетонних блоків, було побудовано дев’ять різних числових моделей відстані вибуху, і кількість вибухівки становила 2 кг. Таблиця 4 узагальнює кінцевий стан пошкодження стін з газобетонних блоків при різних відстанях вибуху. Зі збільшенням відстані вибуху площа пробивного отвору стіни спочатку збільшувалася, а потім зменшувалася. У цих прикладах розрахунків пошкоджена площа була зосереджена в середній частині стіни. Зі збільшенням відстані вибуху площа пробивного отвору спочатку збільшувалася, а потім зменшувалася. Коли співвідношення відстані вибуху до радіуса заряду перевищувало 30, вибухове навантаження на поверхні стіни значно знижувалося, що було меншим за силу зчеплення між розчином і блоками. Тільки центральна зона трохи перевищувала міцність на стиск газобетону, що викликало незначне лущення на поверхні кількох блоків. Тому зі збільшенням відстані вибуху режим руйнування стіни з газобетонних блоків змінювався від сильного пробивного руйнування до незначного лущення.
| Еквівалент вибухівки, кг | Відстань вибуху, м | Відстань у масштабі м/кг1/3 | R/RW | Остаточний стан пошкодження |
| 2 | 0.5 | 0.397 | 7.53 | Площа пробивання отвору 3.48 м2 |
| 2 | 0.6 | 0.476 | 9.03 | Площа пробивання отвору 3.90 м2 |
| 2 | 0.7 | 0.556 | 10.54 | Площа пробивання отвору 3.96 м2 |
| 2 | 0.8 | 0.635 | 12.05 | Площа пробивання отвору 4.23 м2 |
| 2 | 0.9 | 0.714 | 13.55 | Площа пробивання отвору 4.14 м2 |
| 2 | 1.0 | 0.794 | 15.06 | Площа пробивання отвору 3.58 м2 |
| 2 | 1.25 | 0.992 | 18.82 | Площа пробивання отвору 2.58 м2 |
| 2 | 1.50 | 1.191 | 22.59 | Площа пробивання отвору 2.06 м2 |
| 2 | 2.00 | 1.587 | 30.11 | Площа лущення 0.53 м2 |
Таблиця 4. Стан ступеню пошкодження кладки стіни АНБ при різних відстанях до вибуху.
Рисунок 10 показує кінцеві пошкодження стін з газобетонних блоків при відстанях вибуху 0,5, 0,8 і 1,5 м. Коли відстань вибуху становила 0,5 м, велика кількість фрагментів утворилася через високе вибухове навантаження в середній частині стіни, що перевищувала міцність блоку на стиск. Слабке вибухове навантаження в крайовій частині стіни не викликало руйнування блоків; однак деякі блоки були зміщені через руйнування контактних поверхонь, що призвело до утворення пробивного отвору. Коли відстань вибуху збільшилася до 0,8 м, вибухове навантаження в середній частині стіни відносно зменшилося, і кількість фрагментів відносно зменшилася. Однак кількість блоків, які відпали зі стіни, збільшилася, що спричинило збільшення площі пробивного отвору. Коли відстань вибуху збільшилася до 1,5 м, в середній зоні стіни було виявлено мало фрагментів, а площа блоків, які відпали зі стіни, відносно зменшилася, що призвело до зменшення площі пробивного отвору. Причиною цього явища було те, що коли відстань вибуху була малою, енергія, утворена вибухом, головним чином діяла на середню частину стіни. Міцність матеріалу блоків відігравала основну роль у протистоянні вибуху, а міцність зчеплення між блоками відігравала незначну роль. Зі збільшенням відстані вибуху енергія вибуху, що діє на стіну, поступово зменшувалася, а вибухове навантаження, розподілене по стіні, ставало більш однорідним. Частка енергії вибуху, що розсіюється міцністю матеріалу блоків, поступово зменшувалася, а частка енергії вибуху, що розсіюється міцністю зчеплення між блоками, поступово збільшувалася. Тому площа стиснених блоків поступово зменшувалася, а діапазон блоків, які відпали зі стіни, поступово збільшувався, що спричиняло збільшення площі пробивного отвору в стіні. При подальшому збільшенні вибуху міцність зчеплення між блоками відігравала основну роль у протистоянні вибуховому навантаженню. Через зменшення енергії вибуху на стіні діапазон блоків, які відпали зі стіни, поступово зменшувався, і площа пробивного отвору в стіні з газобетонних блоків зменшувалася.
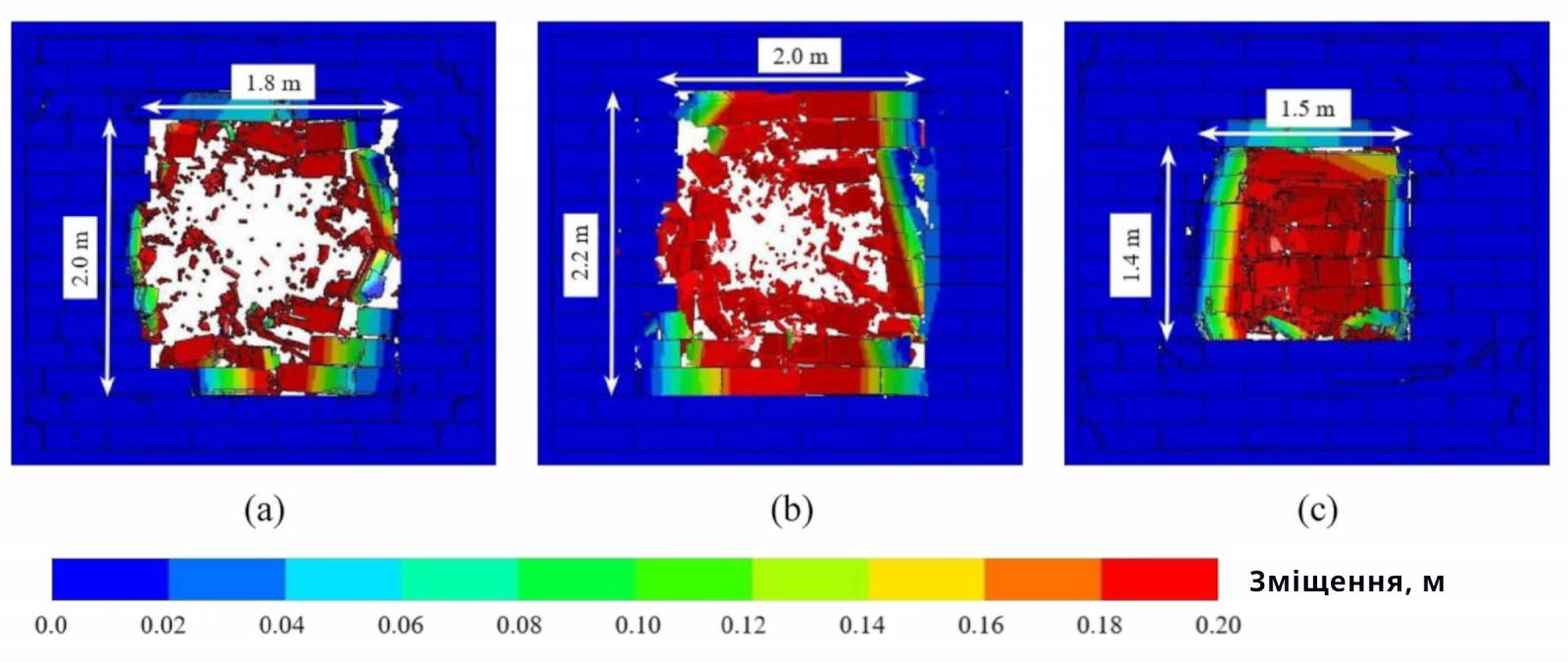
Рисунок 10. (a) Остаточне пошкодження кладки стіни АНБ, коли відстань вибуху становила 0,5 м;
(b) остаточне пошкодження кладки стіни АНБ при відстані вибуху 0,8 м;
(c) остаточне пошкодження кладки стіни АНБ при відстані вибуху 1,5 м.
Рисунок 11 показує розподіл пікових значень відбивного надлишкового тиску вздовж висоти стіни за наведеними трьома умовами. Результати показали, що надлишковий тиск у середній частині стіни поступово зменшувався зі збільшенням відстані вибуху, а концентрація навантаження на стіні поступово збільшувалася, що спричиняло розширення діапазону навантаження контактної поверхні між блоками. Тому площа блоків, які відпали зі стіни, збільшувалася. При подальшому збільшенні відстані вибуху, вибухове навантаження на стіні зменшувалося і мало більш рівномірний розподіл. Діапазон вибухового навантаження, яке спричинило руйнування контактної поверхні між блоками, зменшувався, і ступінь пошкодження стіни зменшувався також. Це ще раз показало, що при постійному еквіваленті вибуху, ступінь пошкодження стіни з газобетонних блоків спочатку збільшувався, а потім зменшувався зі збільшенням відстані вибуху.
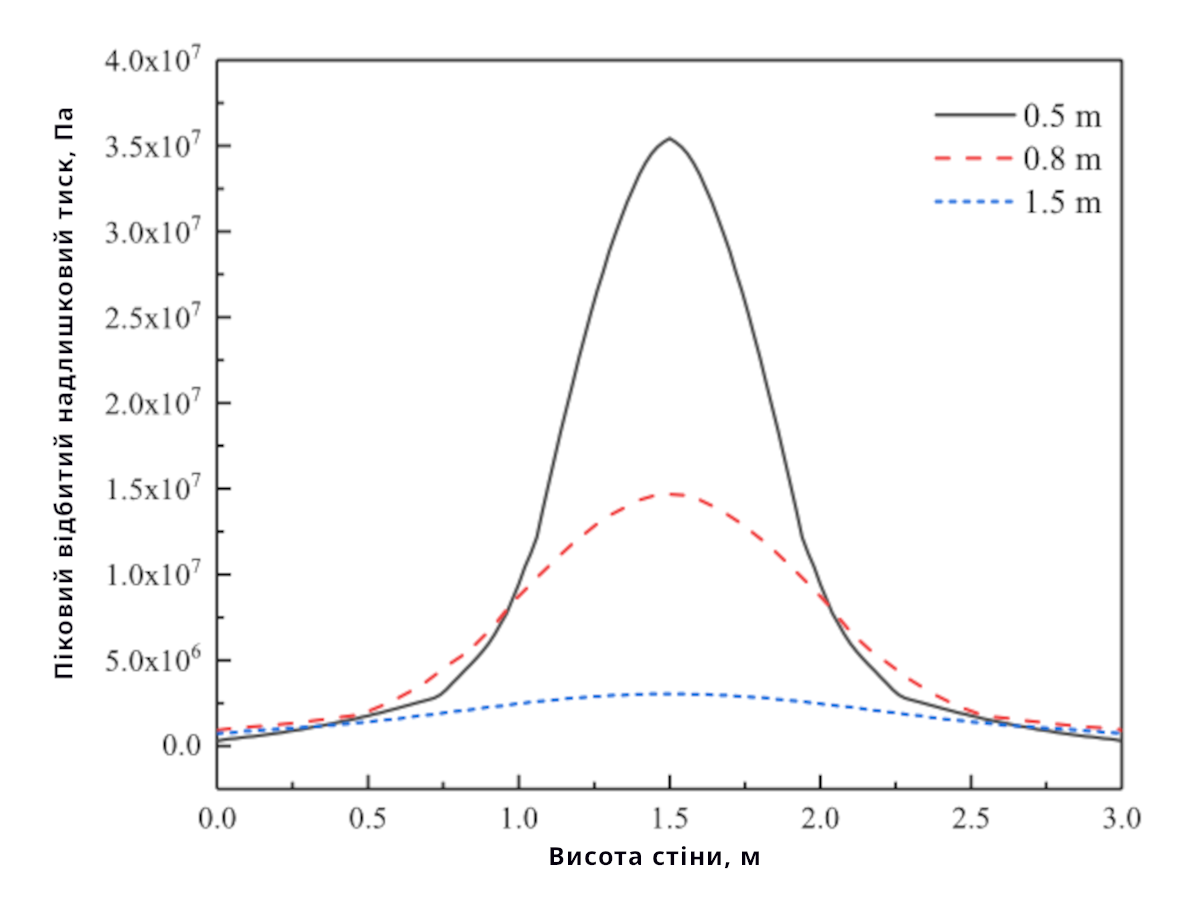
Рисунок 11. Розподіл пікового значення відбитого надлишкового тиску по висоті стіни з різною
відстанню до вибуху.
Оцінка пошкоджень
Розумне визначення критерію відмови є важливою передумовою для оцінки ступеня пошкодження структурних елементів. Зазвичай використовувані критерії відмови для кам'яних стін включають масштабовану відстань, граничне зміщення стіни та кут повороту опори. Однак ці критерії відмови можуть лише оцінити, чи буде пошкоджена кам'яна стіна, але не можуть оцінити ступінь пошкодження кам'яної стіни. У цьому розділі ми запропонували критерій пошкодження, заснований на площі пробивання стіни, який використовується для оцінки ступеня пошкодження кам'яної стіни під дією близького вибухового навантаження.
Метод розрахунку площі пробивання в кам'яній стіні
Механізм пошкодження кам'яних стін під дією близького вибухового навантаження відрізняється від механізму пошкодження однорідної структури. Для аналізу площі пробивання кам'яної стіни під дією близького вибухового навантаження були запропоновані такі припущення. (1) Вибуховий заряд розташований перед центром передньої поверхні стіни, щоб забезпечити нульовий кут падіння під час розповсюдження вибухової ударної хвилі та її впливу на передню поверхню стіни. (2) Час досягнення вибухової ударної хвилі кожної точки стіни нехтується. (3) Тертя між розчином і блоками нехтується.
Як згадувалося раніше, поперечний розмір площі пробивання кам'яної стіни під дією близького вибухового навантаження є цілим числом або напівцілим числом довжини блоку, а поздовжній розмір складається з цілого числа висоти блоку. Для спрощення цього аналізу поверхня з нульовою товщиною була вставлена в середину блоку, щоб перетворити цілий блок на два півблоки, як показано на рис. 12.
Через симетрію навантаження та структури була проаналізована 1/4 частина структури. Під дією близького вибухового навантаження блоки в середній частині кам'яної стіни були роздроблені через високий тиск, а блоки в крайовій зоні відвалювалися від стіни через пошкодження з'єднувальної поверхні між розчином та блоками. Тому площа пробивання кам'яної стіни визначається в основному міцністю з'єднання між розчином та блоками. Було встановлено систему координат з центром кам'яної стіни як початковою точкою, блоки були пронумеровані та проаналізовані, як показано на рис. 13. З'єднувальна сила I та вибухове навантаження F блоку визначалися за формулами:
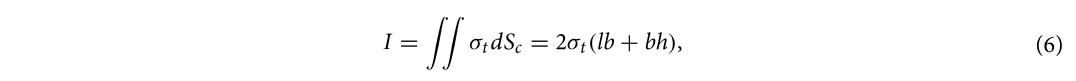
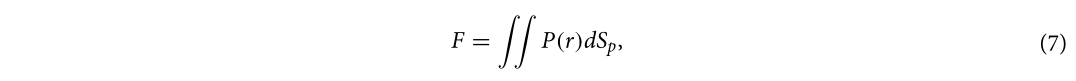
де σt — це міцність з'єднання між розчином і блоком, Sc — площа контакту між розчином і блоком, l, b і h позначають довжину, ширину і висоту блоку відповідно, а Sp — фронтальна вибухова поверхня. Коли вибухове навантаження на блок перевищувало силу з'єднання, блоки відвалювалися від стіни.
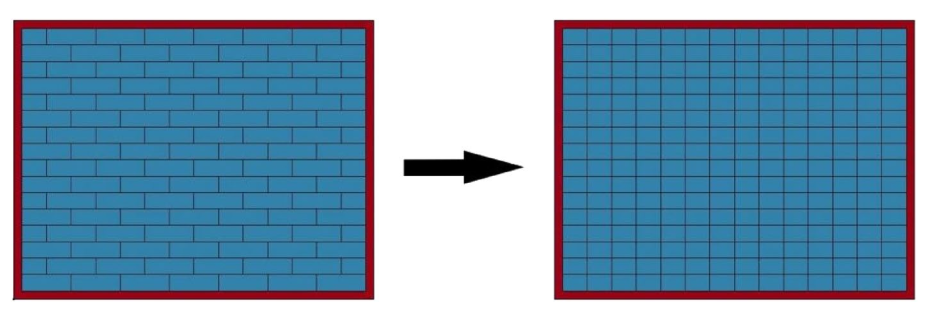
Малюнок 12. Модель аналізу мурованої стіни.
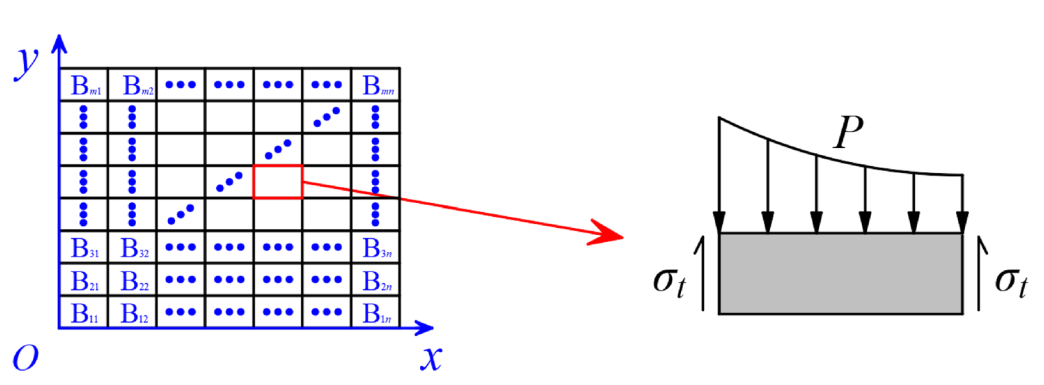
Рисунок 13. Модель аналізу пробивного руйнування кам'яної стіни.
Для заданих робочих умов були отримані такі дані: m (ряди блоків), n (стовпці блоків), l0 (довжина блоку), b0 (ширина блоку), h0 (висота блоку), σt0 (міцність зв'язку) і P0 (вибухове навантаження). Потім ми підставили l0, b0, h0 і σt0 в рівняння (6), щоб отримати I0, і підставили P0 в рівняння (7), щоб знайти F0. Процес визначення кутового блоку Bedge у зоні пробивного отвору був таким:
1. Якщо Imn < Fmn, блок Bmn знаходився в куті пробивного отвору.
2. Якщо Imn ≥ Fmn, слід порівняти співвідношення Im−1n−1 та Fm−1n−1 для блоку Bm−1n−1.
3. Якщо Im−1n−1 < Fm−1n−1, необхідно порівняти співвідношення Imn−1 та Fmn−1 для блоку Bmn−1 і співвідношення Im−1n та Fm−1n для блоку Bm−1n.
- Якщо Imn−1 < Fmn−1, Im−1n ≥ Fm−1n, то блок Bmn−1 знаходився в куті пробивного отвору.
- Якщо Imn−1 ≥ Fmn−1, Im−1n < Fm−1n, то блок Bm−1n знаходився в куті пробивного отвору.
; - Якщо Imn−1 ≥ Fmn−1, Im−1n ≥ Fm−1n, то блок Bm−1n−1 знаходився в куті пробивного отвору.
4. Якщо Im−1n−1 ≥ Fm−1n−1, слід порівняти співвідношення Im−2n−2 та Fm−2n−2 для блоку Bm−1n−1, доки не буде визначено блок у куті пробивного отвору.
Припустимо, що горизонтальна відстань від верхнього правого кута Bedge до центру стіни була L, а поздовжня відстань - H, площу пробивного отвору S кам'яної стіни можна було отримати за допомогою:
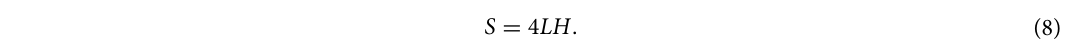
Таблиця 5 показує порівняння між числовими та розрахунковими результатами площі пробивного отвору в мурованій стіні в розділі "Динамічна відповідь мурованої стіни з AНБ під дією близького вибуху", що вказує на те, що більшість розрахункових результатів були вищими за числові. Це було обумовлено тим, що в цьому припущенні було нехтувано тертям між поверхнею зв'язку, розчином і блоками, а обмежувальна сила блоку в розрахунковій моделі була меншою за фактичну обмежувальну силу. В результаті, розрахована площа пробивного отвору була більшою за числові результати. Помилка між числовими та розрахунковими результатами не перевищувала 15%, що відповідало фактичним інженерним вимогам. Тому розрахунковий метод площі пробивного отвору в кам'яній стіні, запропонований у цьому розділі, є ефективним.
| Еквівалент вибухівки, кг | Відстань до вибуху, м | Числовий результат, м2 | Розрахунковий результат, м2 | Похибка, % |
| 1 | 0.5 | 1.59 | 1.80 | 13.21 |
| 1.0 | 0.56 | 0.54 | -3.57 | |
| 1.5 | - | - | - | |
| 2.0 | - | - | - | |
| 2 | 0.5 | 3.48 | 3.60 | 3.45 |
| 1.0 | 3.58 | 3.78 | 5.59 | |
| 1.5 | 2.06 | 2.10 | 1.94 | |
| 2.0 | 0.53 | 0.60 | 13.2 |
Таблиця 5. Порівняння числових результатів і результатів розрахунку зони руйнування продавлювання кладки стіни з АНБ.
Метод розрахунку площі пробивного отвору в кам'яній стіні
Згідно з числовими результатами, пошкодження кам'яної стіни з AНБ можна розділити на такі ступені:
(a) слабке пошкодження, коли відбулося незначне відшарування на передній та задній поверхнях стіни, і жоден блок не випав зі стіни;
(b) середнє пошкодження, коли відбулося серйозне відшарування на передній та задній поверхнях стіни, і декілька відносно цілих блоків випали зі стіни;
(c) сильне пошкодження, коли велика кількість блоків випала зі стіни;
(d) пошкодження з обвалом, коли стіна повністю розвалилася та обвалилася.
Згідно з числовими результатами, можна отримати емпіричний критерій пошкодження кам'яних стін з AНБ під дією близького вибуху. Параметр пошкодження D може бути визначений як
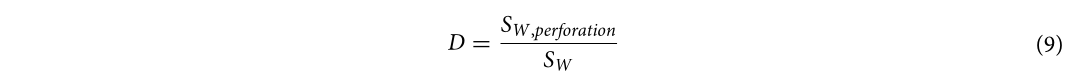
де Sw, perforation— це площа пробивного отвору, а Sw — площа поверхні стіни. Коли 0 < D ≤ 0,2, стіна зазнає слабкого ступеня пошкодження; коли 0,2 < D ≤ 0,5, стіна зазнає середнього ступеня пошкодження; коли 0,5 < D ≤ 0,8, стіна зазнає сильного ступеня пошкодження; коли 0,8 < D ≤ 1, стіна зазнає ступеня пошкодження з обвалом. Кінцеві умови руйнування кам'яних стін з AНБ з різними ступенями пошкодження показано на рис. 14.
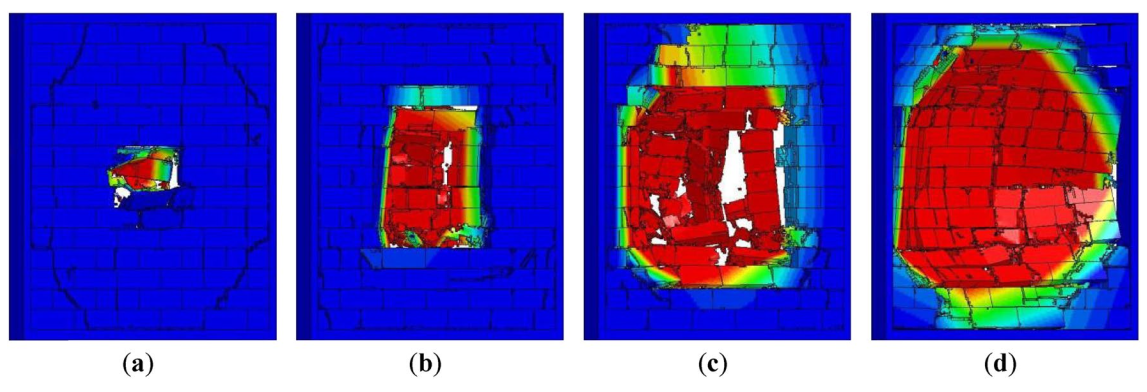
Малюнок 14. (a) Слабке пошкодження; (b) середнє пошкодження; (c) сильне пошкодження; (d) пошкодження з обвалом.
Висновки
У цьому дослідженні ми вивчали процес динамічної відповіді та характеристики руйнування стін з газобетону (AНБ) під дією вибухового навантаження. Було побудовано повномасштабну тривимірну кінцевоелементну модель стіни з газобетону, і точність чисельної моделі була перевірена шляхом порівняння з попередніми експериментальними результатами. У цьому дослідженні були проаналізовані процес руйнування та режим руйнування стіни з газобетону. Були обговорені впливи різних розмірів блоків, товщини стін, міцності клейового розчину на стиск і відстані до вибуху на ступінь пошкодження стіни з газобетону. Згідно з аналітичними результатами можна зробити наступні ключові висновки:
1. Режим руйнування та ступінь пошкодження чисельної моделі стіни з газобетону були узгоджені з експериментальними результатами, що вказує на те, що запропонований чисельний метод може точно моделювати динамічну відповідь та поведінку пошкодження стін з газобетону під дією вибухового навантаження. Стіна з газобетону демонструвала місцеві пробивні пошкодження під дією близького вибуху.
2. Зі зменшенням розміру блоку ступінь пошкодження стіни з газобетону зменшувався, причому горизонтальна жорсткість блоку відігравала більшу роль, ніж вертикальна жорсткість. Однак вплив розміру блоку на вибухостійкість стін з газобетону був дуже обмеженим.
3. Зі збільшенням товщини стін збільшувалися момент інерції секції, паралельної до напрямку вибухового навантаження, та зв’язуюча сила між клейовим розчином і блоками, що значно підвищувало зсувну стійкість стіни. Площа пробивної ділянки відносно зменшувалася, а форма пробивної ділянки змінювалася з круглої на квадратну. Збільшення товщини стіни дозволяло зменшити ступінь пошкодження стіни з газобетону під дією близького вибуху.
4. Зі збільшенням міцності клейового розчину на стиск збільшувалася зв’язуюча міцність між розчином і блоками, що призводило до покращення цілісності стіни з газобетону та збільшення ефекту дисипації вибухової енергії, а також до зменшення максимального відхилення та ступеня пошкодження стіни з газобетону. Підвищення міцності розчину на стиск дозволяло стіні покращити структурну стійкість до вибухового пошкодження.
5. При незмінному еквіваленті вибуху і збільшенні відстані до вибуху дисипація вибухової енергії змінювалася від міцності матеріалу блоку до зв’язуючої міцності між розчином і блоками, де ступінь пошкодження стін з газобетону спочатку збільшувався, а потім зменшувався. Тому потрібно повністю враховувати комбіновані ефекти еквіваленту вибуху та відстані до вибуху при оцінці ступеня пошкодження стін з газобетону.
6. Було встановлено метод обчислення площі пробивної ділянки мурованих стін під дією близького вибухового навантаження, і ефективність методу було перевірено порівнянням з чисельними результатами. Було запропоновано критерій пошкодження на основі площі пробивної ділянки стіни з газобетону для оцінки ступеня пошкодження стіни під дією близького вибухового навантаження. Цей метод може надати теоретичну базу для дослідження дисипації вибухової енергії мурованими стінами з газобетону у майбутньому.
Список літератури
1. Naito, C., Olmati, P., Trasborg, P., Davidson, J. & Newberry, C. Assessment of insulated concrete walls to close-in blast demands. J. Perform. Construct. Facil. 29(6), 04014149 (2014).
2. Li, J., Wu, C. & Hao, H. Experimental investigation of ultra-high performance concrete slabs under contact explosions. Int. J. Impact Eng. 93, 62–75 (2016).
3. Cormie, D., Mays, G. & Smith, P. Blast Effects on Buildings (ICE Publishing, 2019).
4. Hao, H., Hao, Y., Li, J. & Chen, W. Review of the current practices in blast-resistant analysis and design of concrete structures. Adv. Struct. Eng. 19(8), 1193–1223 (2016).
5. Ekstrom, J., Rempling, R. & Plos, M. Spalling in concrete subjected to shock wave blast. Eng. Struct. 122, 72–82 (2016).
6. Shamim, S., Ahmad, S. & Khan, R. A. Numerical modelling of masonry panel subjected to surface blast loading. J. Xi’an Univ. Arch. Technol. 12(7), 846–857 (2020).
7. Shamim, S., Ahmad, S. & Khan, R. A. Finite element analysis of masonry wall subjected to blast loading. Int J Adv Mech Civ Eng 6, 50–53 (2019).
8. Ahmad, S. et al. Experimental study of masonry wall exposed to blast loading. Mater Constr 64, e007 (2014).
9. Knock, C. et al. The bounce and roll of masonry debris. Int. J. Impact Eng. 30(1), 1–16 (2004).
10. Shi, Y., Xiong, W., Li, Z.-X. & Qingfeng, Xu. Experimental studies on the local damage and fragments of unreinforced masonry walls under close-in explosions. Int. J. Impact Eng. 90, 122–131 (2016).
11. Li, Z. et al. Experimental and numerical study on CFRP strip strengthened clay brick masonry walls subjected to vented gas explo- sions. Int. J. Impact Eng. 129, 66–79 (2019).
12. Shamim, S., Khan, R. A. & Ahmad, S. Fragility analysis of masonry wall subjected to blast loading. Structures 39, 1016–1030 (2022).
13. Shamim, S., Ahmad, S. & Khan, R. A. Blast vulnerability of multi-storey masonry infill reinforced concrete frames. Civ. Eng. Archit. 9(3), 853–868 (2021).
14. Shamim, S., Ahmad, S. & Khan, R. A. An investigation on response of blast load on masonry structure. Lect. Notes Civ. Eng. 58, 527–538 (2019).
15. Shamim, S., Ahmad, S. & Khan, R. A. Numerical study on dynamic response of hollow and cavity type clay brick masonry infill panels subjected to blast loading. Eng. Failure Anal. 146, 107104 (2023).
16. Raza, I., Shamim, S., Ahmad, S. & Khan, R. A. Isotropic modelling and blast analysis of heritage structure. Mater. Today Proc. 66, 2547–2553 (2022).
17. Raza, I., Shamim, S., Ahmad, S. & Khan, R. A. Analysis of two-storey masonry structure under blast loading. Mater. Today Proc. 80, 1605–1610 (2023).
18. Shamim, S., Ahmad, S. & Khan, R. A. Dynamic response of masonry panel under high-strain loading condition. Adv. Struct. Mech. Appl. 26, 78–89 (2022).
19. Wu, C. & Hao, H. Derivation of 3D masonry properties using numerical homogenization technique. Int. J. Numer. Methods Eng. 66(11), 1717–1737 (2010).
20. Ma, G., Hao, H. & Lu, Y. Homogenization of masonry using numerical simulations. J. Eng. Mech. 127(5), 421–431 (2001).
21. Macorini, L. & Izzuddin, B. A. Nonlinear analysis of unreinforced masonry walls under blast loading using mesoscale partitioned modeling. J. Struct. Eng. 140(8), A4014002.1-A4014002.10 (2014).
22. Formica, G., Sansalone, V. & Casciaro, R. A mixed solution strategy for the nonlinear analysis of brick masonry walls. Comput. Methods Appl. Mech. Eng. 191(51), 5847–5876 (2002).
23. Hamed, E. & Rabinovitch, O. Nonlinear dynamic behavior of unreinforced masonry walls subjected to out-of-plane loads. J. Struct. Eng. 134(11), 1743–1753 (2008).
24. Wittmann FH, Balkema A. Advances in autoclaved aerated concrete. Citeseer 1992.
25. Narayanan, N. & Ramamurthy, K. Structure and properties of aerated concrete: A review. Cem. Concr. Compos. 22, 321–329 (2000).
26. Guo, Q., Gou, Y., Chen, J., Zhang, Y. & Zhou, Y. Dynamic response of foam concrete under low-velocity impact: Experiments and numerical simulation. Int. J. Impact Eng. 146, 103693 (2020).
27. Feng, S., Zhou, Y., Wang, Y. & Lei, M. Experimental research on the dynamic mechanical properties and damage characteristics of lightweight foamed concrete under impact loading. Int. J. Impact Eng. 140, 103558 (2020).
28. Nian, W., Subramaniam, K. V. L. & Andreopoulos, Y. Experimental investigation on blast response of cellular concrete. Int. J. Impact Eng. 96, 105–115 (2016).
29. Yankelevsky, D. Z. & Avnon, I. Autoclaved aerated concrete behavior under explosive action. Construct. Build. Mater. 12, 359–364 (1998).
30. Li, Z. et al. Experimental and numerical study of basalt fiber reinforced polymer strip strengthened autoclaved aerated concrete masonry walls under vented gas explosions. Eng. Struct. 152, 901–919 (2017).
31. Li, Z. et al. Study of autoclaved aerated concrete masonry walls under vented gas explosion. Eng. Struct. 141, 444–460 (2017).
32. Yu, Q. et al. Experimental and numerical investigation of polymer-reinforced and normal autoclaved aerated concrete masonry walls under large TNT explosive loads. Int. J. Impact Eng. 164, 104188 (2022).
33. Mollaei, S., Babaei Ghazijahani, R. & Noroozinejad Farsangi, E. Investigation of behavior of masonry walls constructed with autoclaved aerated concrete blocks under blast loading. Appl. Sci. 12, 8725 (2022).
34. General Administration of Quality Supervision Inspection and Quarantine of PR China, General Code for Masonry Structure (GB 55007-2021) (Standards Press of China, Beijing, 2021).
35. David, H. W. Usery’s guide for microcomputer programs CONWEP and FUNPRO. Applications of TM5-855-1, fundamentals of protective design for conventional weapons. In Final Report, AD-A195 867 (1988).
36. Halquist, J. LS-DYNA Keyword User’s Manual Version 971 (Livermore Software Technology Corporation, 2007).
 Офіційна Facebook сторінка ВААГ
Офіційна Facebook сторінка ВААГ
